1532. Handshake

Consider a meeting of n businessmen sitting around a circular table. To start the meeting, they must shake hands. Each businessman shakes the hand of exactly one other businessman. All handshakes happen simultaneously. We say that the shake is perfect if no arms cross each other.

Find the number of perfect shakes that exist for n businessmen.

Input. Each line contains one even integer n (2 ≤ n ≤ 50).

Output. For each value of n print in a separate line the number of perfect shakes that exist for n businessmen.

Sample input	Sample output
2 4 8	1 2 14

SOLUTION

Catalan numbers

Algorithm analysis

Let’s number the businessmen sitting at the table with numbers 1, 2, ..., 2 * p = n. Denote by f(p) the number of ways in which they can shake hands according to the condition of the problem. Consider all possible handshakes of the first businessman. He can only extend his hand to the businessman who has an even number. If the first businessman extends his hand to (2 * k) - th, then from one side of their hands intersection there will be 2 * k – 2 people who can shake hands in f(k – 1) ways, and on the other side 2 * p – 2 * k people who can shake hands in f(p – k) ways.

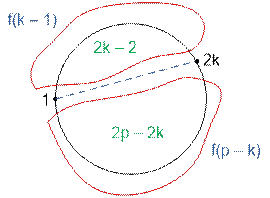
Choosing k = 1, 2, …, p, we get:

f(p) = f(0) * f(p – 1) + f(1) * f(p – 2) + … + f(k – 1) * f(p – k) + … + f(p – 1) * f(0),

f(1) = 1, f(0) = 1

That is, f(p) = are Catalan numbers.

The answer to the problem is the value f(n / 2).

Example

The values of the Catalan numbers are calculated in the cat array according to the formula above:

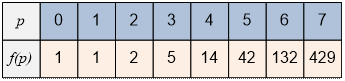
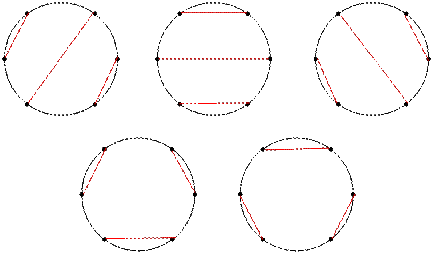
For example, n = 6 businessmen can shake hands in f(3) = 5 ways.

Algorithm realization

In the cat[i] cells, we will calculate the i-th Catalan number.

long long cat[51];

Using the recursive formula f(p) = , function countPerfect finds the Catalan numbers from zero to n-th.

void countPerfect(int n)

{

int i, j;

cat[0] = cat[1] = 1;

for(i = 2; i <= n; i++)

for(j = 0; j < i; j++)

cat[i] += cat[j] * cat[i - j - 1];

}

The main part of the program. For each input value n print cat[n / 2].

countPerfect(50);

while(scanf("%d",&n) == 1)

printf("%lld\n",cat[n/2]);

Java realization

import java.util.*;

public class Main

{

static long[] countPerfect(int n)

{

int i, j;

long cat[]= new long[51];

cat[0] = cat[1] = 1;

for(i = 2; i <= n; i++)

for(j = 0; j < i; j++)

cat[i] += cat[j] * cat[i - j - 1];

return cat;

}

public static void main(String[] args)

{

long cat[] = countPerfect(50);

Scanner con = new Scanner(System.in);

while(con.hasNext())

{

int n = con.nextInt();

System.out.println(cat[n/2]);

}

}

}